Dimensionando um telescÓpio Dobsoniano

Introdução
Fundamentos da Óptica Geométrica
Reflexão no espelho plano
Reflexão no espelho esférico
A Configuração Óptica do Telescópio Newtoniano
A Configuração Mecânica Dobson
O conceito desenvolvido por John Dobson une a configuração telescópica newtoniana com o sistema de coordenadas altazimutais.
O telescópio newtoniano desenvolvido por Issac Newton em 1668 representa uma grande simplificação nos elementos ópticos com relação a outras configurações. A objetiva é somente um espelho esférico côncavo ao contrário dos telescópios refratores compostos por uma ou mais lentes para eliminar as aberrações cromáticas. A inclusão do espelho secundário permite desviar o feixe a noventa graus e observar os objetos celestes numa posição radial ao eixo óptico do espelho primário.
O sistema de coordenas horizontal ou altazimutal permite uma montagem mecânica simples - apesar de não podermos compenssar o efeito da rotação terrestre com simplicidade - de baixo custo e, bem leve quando nós comparamos com uma similar a montagem equatorial ou montagem tradicional alemã.
Para aqueles que desejam construir um telescópio dobsoniano, nós vamos dividir o processo de construção do telescópio em algumas etapas a saber:
A Configuração Óptica
A Configuração Mecânica
Das duas nós faremos uma série de considerações que nos levarão ao dimensionamento da montagem mecânica do telescópio. O nosso objetivo será estabeler os parâmetros necessários - os compromissos - entre a óptica e a mecânica do conjunto para nós obtermos a melhor eficiência do telescópio. Esse compromisso entre óptica e mecânica será dirigido para um telescópio dobsoniano de observação visual. Não vamos nos preocupar aqui com adaptações e/ou configurações para máquinas fotográficas ou qualquer outro dispositivo adicional.
Fundamentos da Óptica Geométrica
Um curso formal sobre óptica geométrica que atenda aas necessidades reais para trabalharmos a ótica do telescópio newtoniano será muito longo. No intuito de sermos breves, nós introduziremos os conceitos mínimos necessários para que o traçado de raios possa ser compreendido. Para isso nós precisamos saber:o que é a reflexão de um raio por um espelho plano e,
a partir de dois raios com comportamentos conhecidos no espelho esférico côncavo
elaborar e construir a teia de raios e feixes que nós permitiremos avaliar a configuração óptica newtoniana.
Reflexão no Plano
Nós todos estamos acostumados com a nossa imagem através de um espelho. Cada ponto do nosso rosto "emana raios" que atingem a superfície refletora do espelho e retorno aos nossos olhos. A natureza é muito sábia e no processo de reflexão e mesmo no de refração da luz, ela, a LUZ, percorre o menor caminho. Essa propriedade é conhecida como o Princípio de Fermat. Esse princípio é muito fácil de ser percebido na reflexão. Observe a figura abaixo:
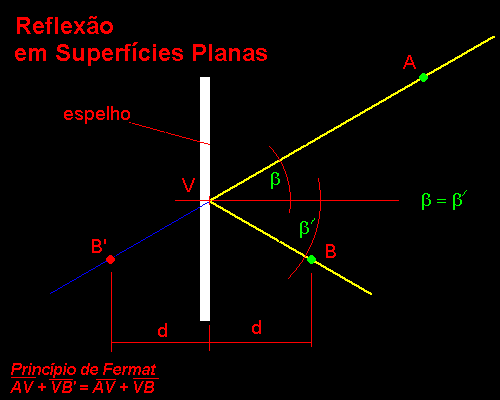
Fig.01- A Reflexão em superfícies planasO raio de luz que passa por A atinge o ponto de incidência V no espelho plano e é desviado por um ângulo exatamente igual, mas contrário em relação à normal (perpendicular a superfície do espelho em V). Os ângulos b e b'são iguais. Observe que os pontos B e B' marcados sobre o raio refletido e o segmento auxiliar respectivamente são eqüidistantes em relação ao espelho. O comprimento do segmento AB' é o segmento AV+ VB' e este é exatamente igual ao comprimento do segmento AV + VB. O percurso da luz de A até B foi feito pelo menor caminho. Se nós tomarmos qualquer outro ponto do espelho que não seja o V, o caminho de A até B será sempre maior. Da Geometria plana, dado dois pontos não coincidentes, nós sempre teremos um segmento de reta ou uma única reta passando por esses dois pontos.
Reflexão no Espelho Esférico CôncavoOs raios importantes para traçar o feixe de luz que atinge um espelho esférico côncavo são dois:
Raio paralelo ao eixo óptico
Raio incidente no vértice do espelho
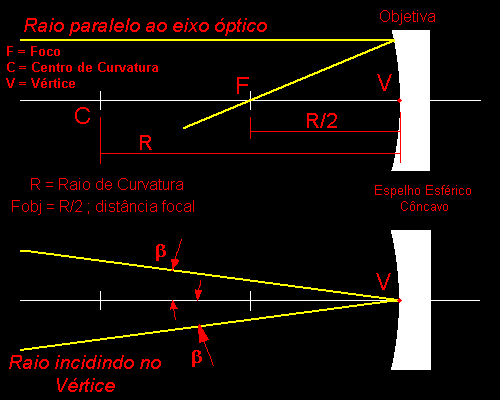
Fig.02- Raios principais do espelho esférico côncavoNote que o vértice V é o ponto central de simetria radial da superfície esférica do espelho e por ele passa o eixo óptico do espelho (linha branca) da direção axial (ao longo do eixo). No caso da superfície esférica C é o centro de curvatura e no caso com raio R. Para esse tipo de superfície refletora, todo raio que chega paralelo ao eixo ótico é desviado em direção ao ponto F (foco). Todos os raios paralelos convergem para o ponto F distante R/2 do vértice V do espelho.
Outro raio importante é o que incide exatamente no vértice do espelho. Nesse ponto o raio incidente tem o seu raio refletido desviado do mesmo valor da incidência em relação ao eixo óptico. Veja que nesse caso o vértice V do espelho côncavo funciona como um espelho plano nesse local.
O mesmo ocorre para os raios que chegam paralelo ao eixo óptico. Eles ao incidirem na superfície do espelho, a reflexão deverá naquele ponto ser aplicada e o raio será desviado para o ponto F (foco).
Tudo isso que nós estamos afirmando para o espelho côncavo é uma aproximação e é válido para ângulos pequenos - da ordem de cinco graus.Com esses dois elementos básicos, nós passaremos a Configuração Óptica do Telescópio Newtoniano. Nela nós veremos o problema da colocação do espelho secundário.
A Configuração Óptica do Telescópio NewtonianoO telescópio refletor newtoniano é composto de um espelho esférico côncavo como indicado na figura abaixo. Tem um eixo de simetria que ao mesmo tempo é o seu eixo óptico.
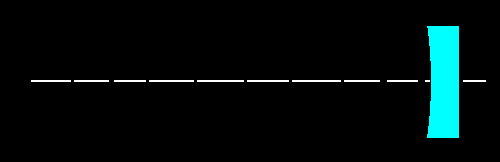
Fig.03- O espelho côncavo esférico.Ao passarmos um feixe de luz paralelo ao eixo óptico, sua luz será toda desviada para um ponto comum sobre o eixo óptico chamado de foco. Esse feixe corresponde a luz vinda de um objeto muito longe, por exemplo, uma árvore muito distante. A LUZ de uma estrela do firmamento corresponde bem a essa situação.
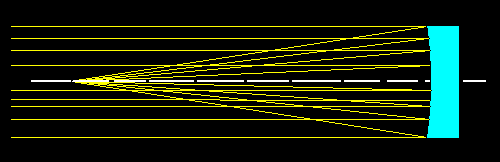
Fig.04- Feixe de luz paralelo ao eixo ópticoNo caso de objetos extensos, ou de objetos muito longe e fora do eixo óptico do espelho primário, a luz desses objetos será tratada como um feixe paralelo, mas inclinado em relação ao eixo de simetria axial. A inclinação desse feixe corresponderá ao campo de visão do telescópio. Na figura abaixo, nós temos a situação de um objeto no infinito e acima do eixo óptico. Por causa da reflexão, a imagem se formará num ponto afastado na direção radial em relação ao foco do espelho primário e se formará do lado contrário do feixe incidente. O espelho irá inverter a imagem.
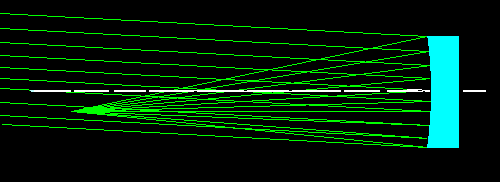
Fig.05- Feixe de luz paralelo, mas inclinado e acima do eixo ópticoDe igual modo, nós vamos traçar os raios de um feixe paralelo inclinado, mas oposto ao da figura anterior. A situação toda se inverte a descrição da figura 05.
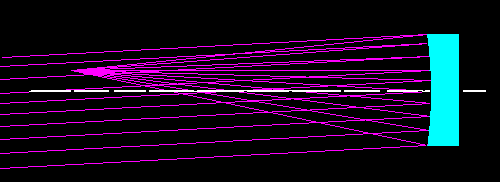
Fig.06- Feixe de luz paralelo, mas inclinado abaixo do eixo óptico.O conjunto de todos esses três feixes paralelos nós mostra como a luz é modificada pelo espelho primário para formar a imagem sobre o plano focal. Se nós montássemos a ocular na frente, ao observar as nossas cabeças irão naturalmente obstruir a luz e nós não veremos nada.

Fig.07- O conjunto de todos os feixes paralelos e o plano focalA solução para esse problema consiste em nós colocarmos um espelho plano inclinado de 45 graus para desviar o feixe em noventa graus em relação ao eixo óptico. Desse modo o plano focal ficará fora da entrada de luz e nós poderemos observá-lo a partir da direção radial. O espelho plano (secundário) deverá ser colocado entre o foco e o vértice do espelho esférico (primário). Na figura abaixo, nós temos a colocação desse novo elemento no sistema óptico.
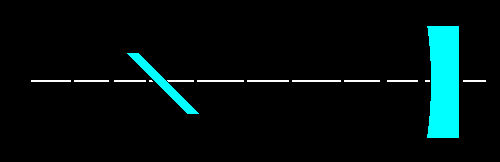
Fig.08- O espelho plano secundário ou espelho diagonalComo nós podemos perceber a introdução de um elemento central a frente o espelho primário causara certa obstrução da luz total incidente. Para o caso o feixe paralelo ao eixo óptico o resultado será:
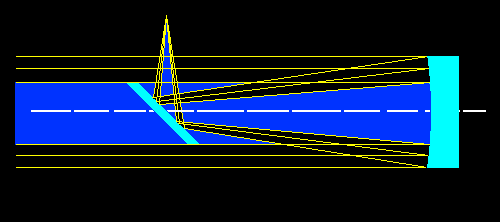
Fig.09- Obstrução do feixe de luz paralelo a eixo ótico.Para o feixe paralelo inclinado acima do eixo óptico, o resultado será:
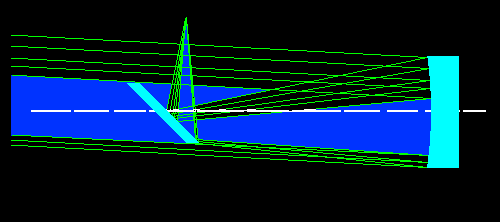
Fig.10- Obstrução do feixe paralelo inclinado acima o eixo ópticoE para o feixe paralelo, mas inclinado abaixo do eixo óptico, nós teremos:
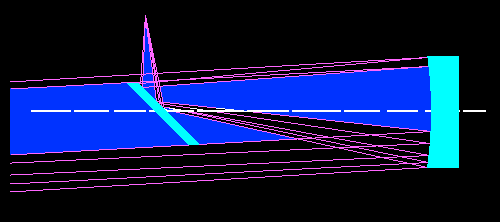
Fig.11- Obstrução do feixe paralelo inclinado abaixo do eixo óptico.Juntando todos os três feixes paralelos, nós teremos a configuração clássica do telescópio refletor newtoniano. Nós temos realmente uma perda de luz e ela será cada vez maior à medida que o espelho secundário se aproximar do espelho primário.
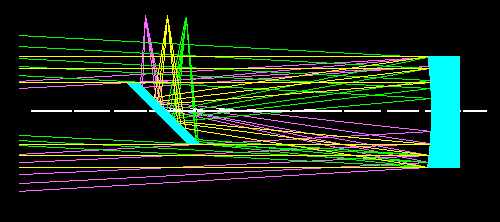
Fig.12- A Configuração óptica de um telescópio newtoniano.Eliminando-se o feixe de raios e ficando somente com os raios externos, nós teremos os elementos geométricos necessário para dimensionar e posicionar o espelho secundário como indicado na figura abaixo.
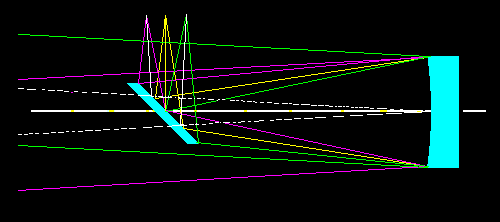
Fig.13- Raios necessários para dimensionar o espelho primário.Observe que na figura abaixo que o recuo (r) do espelho secundário deverá ser maior que a metade do diâmetro do espelho primário. O ângulo 2α será ao campo de visão desejado do telescópio e corresponderá ao deslocamento (2c) sobre o plano focal do feixe paralelo inclinado. A interceptação dos raios externos com o plano do espelho secundário irá determinar a sua dimensão meridional (a).
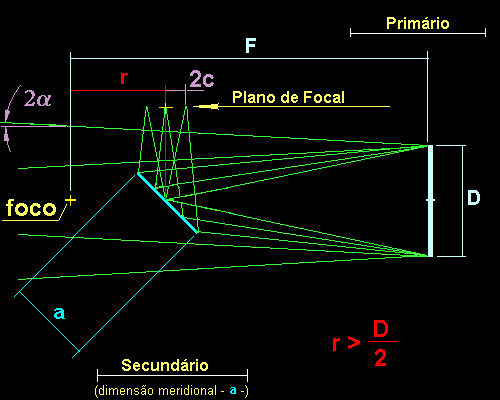
Fig.14- Dimensão meridional do espelho secundárioA outra dimensão do espelho secundário corresponde à direção sagital - plano perpendicular as figuras e que passa pelo eixo óptico. Na figura abaixo, nós temos a representação da direção sagital extraída a partir dos feixes refletidos pelo espelho primário sem o secundário. O segmento transversal perpendicular ao eixo óptico que passa pelo ponto de intersecção do espelho secundário com o eixo óptico do espelho primário corresponderá à dimensão sagital do espelho secundário.No mínimo o nosso espelho secundário será um retângulo com dimensões a e b. A sua forma real é próxima a uma elipse com eixos a e b.
A Configuração Mecânica de John Dobson
A próxima etapa será nos alojarmos o espelho primário numa caixa a CAIXA DO PRIMÄRIO e de igual modo o espelho secundário numa caixa a CAIXA DO SECUNDÁRIO. Observe que as dimensões da caixa deverão ser tais que não haja obstrução dos raios mais externos e que não haja obstrução nos raios que chegam ao plano focal. Também deveremos controlar a separação entre as caixas em função da posição do espelho primário. Por uma questão de estabilidade a caixa do secundário deverá ser feita de uma madeira menos espessa que a da caixa do primário e garantir um equilíbrio estático mais próximo do primário. Veja a figura abaixo:

Fig.15- Colocando as caixas dos espelhosA caixa do espelho primário deverá permitir a fixação e o ajuste da orientação do plano perpendicular ao eixo óptico que passa pelo vértice do espelho. O ajuste desse espelho corresponderá ao caminho óptico da luz refletida no vértice e que deverá atingir o espelho secundário e desviá-la até a ocular.
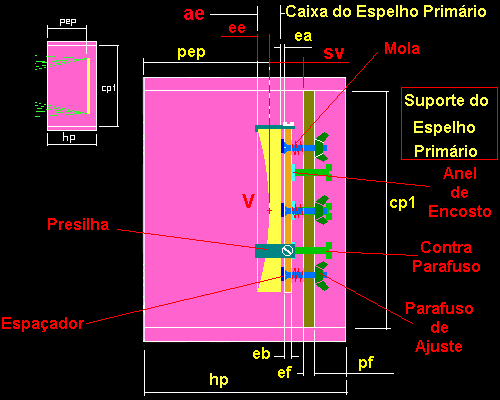
Fig. 16- A Caixa do Espelho Primário e o seu suporte de fixaçãoO suporte do espelho primário consiste num sistema mecânico de apoio sobre três pontos. O parafuso de ajuste permite controlar a orientação do plano radial que passa pelo vértice do espelho primário (V). As molas facilitam o ajuste mantendo a base de fixação do espelho afastada do fundo da caixa. Os contra-parafusos servem para travar a orientação do espelho primário.
A caixa do espelho secundário deverá propiciar a fixação do espelho diagonal e permitir uma mobilidade no posicionamento desse espelho para o ajuste do caminho a ser percorrido pela luz ao longo do eixo óptico central entre a ocular, o espelho secundário e o vértice do espelho primário.
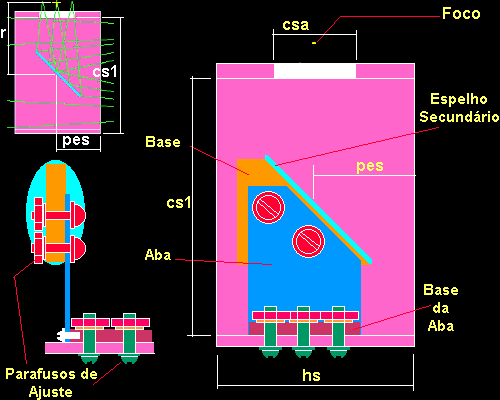
Fig.17- A Caixa do Espelho secundário e o seu suporte de fixaçãoOs parafusos de ajuste permitem centralizar o espelho secundário e orientar a inclinação do mesmo.
Durante o processo de alinhamento, um feixe central vindo a partir do sistema de focalização deverá ser refletido e desviado pelo espelho secundário em direção ao vértice do espelho primário. Em seguida, a orientação do espelho primário deverá ser feita para que o feixe retorne pelo mesmo caminho no sentido do sistema de focalização.
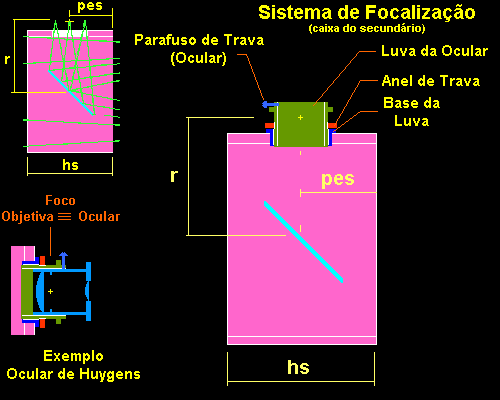
Fig.18 - Sistema de FocalizaçãoO sistema de focalização adotado por nós emprega uma flange de caixa d'água de PVC Marrom de 32 mm. Foram necessárias duas delas para compor o sistema de focalização - o anel de trava foi retirado do que seria a base da luva. O diâmetro de 32 mm corresponde as oculares com bitola 1,25 polegadas de encaixe. O anel de trava é necessário, pois há uma folga muito grande entre a luva e a base da luva por causa do tipo de rosca empregada na flange (rosca dardlet).
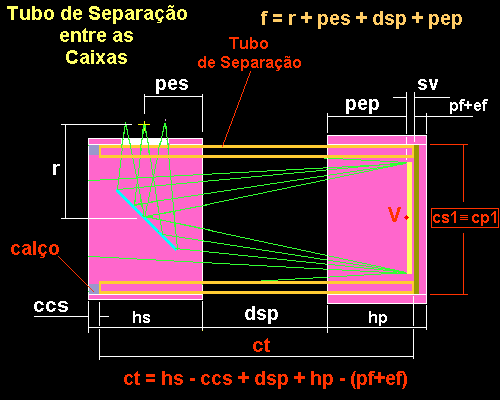
Fig.19 - Separação entre as Caixas (Primário e Secundário)Para manter a separação entre as caixas, nós empregamos tubos de PVC Marrom de 32 mm de diâmetro. Para facilitar a montagem, nós colocamos na caixa do secundário calços de madeira como limitadores. O comprimento dos tubos deverá ser ajustado para que o foco caia no local desejado no sistema de focalização. Na montagem lembre-se de marcar a posição do cano e a qual canto da caixa ele deva ser sempre fixado. Isso é necessário, pois em caso de transporte é necessário montá-los nas respectivas posições para evitar algum deslocamento na montagem e ter que alinhar o conjunto óptico novamente.
Com a montagem do sistema óptico newtoniano acima e incluindo o sistema de focalização e algum sistema de mira de sua escola, nós podemos proceder à determinação da posição do centro de massa ao longo do conjunto. Para isso, nós utilizamos uma cunha e procuramos a posição em que o sistema fica em equílibrio estático.
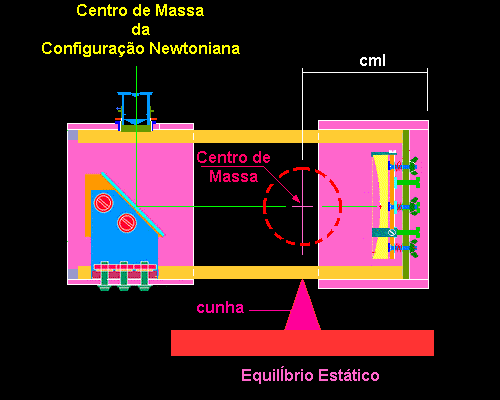
Fig. 20 - Determinando a posição do centro de massa do sistema óptico.Conhecendo a posição do centro de massa, nós colocaremos a articulação do suporte de altura conforme o esquema abaixo.
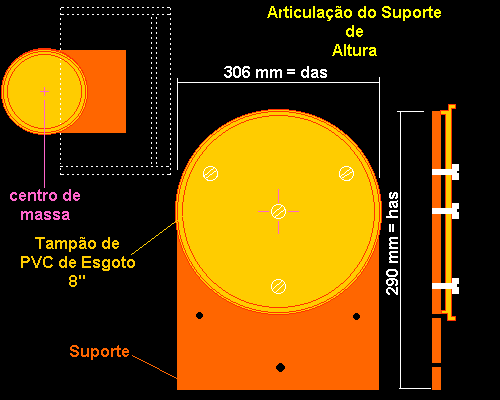
Fig. 21 - Articulação do ajuste de alturaA articulação do ajuste de altura foi construída a partir de um tampão de esgoto de oito polegadas. A vantagem desse diâmetro é a excelente área de contato cujo atrito manterá o telescópio na posição desejada sem qualquer deslocamento. Os deslocamentos não ocorrerão desde que o sistema do conjunto óptico tenha sido balanceado e montado em relação ao centro de massa.
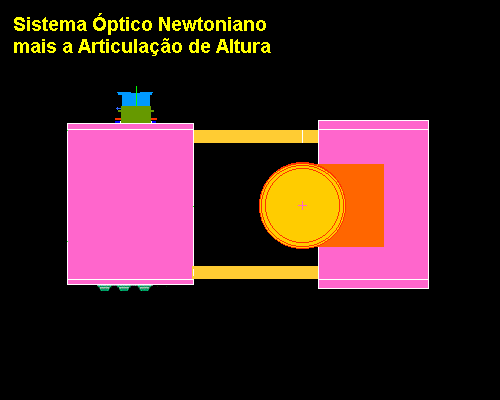
Fig.22 - O sistema óptico newtoniano com o suporte de articulação de alturaO último conjunto da montagem dobsoniana é a montagem da base de articulação do azimute. Nós precisaremos de uma caixa de articulação do azimute onde a articulação, do suporte de altura, possa ser encaixada.
Aprimorando o seu Telescópio Dobsoniano
Retorna a página: O Nosso Telescópio Dobsoniano